12. 矩阵中的路径

牛客网 (opens new window)

题目描述

判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向上下左右移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。

例如下面的矩阵包含了一条 bfce 路径。

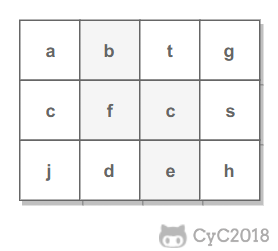
解题思路

使用回溯法（backtracking）进行求解，它是一种暴力搜索方法，通过搜索所有可能的结果来求解问题。回溯法在一次搜索结束时需要进行回溯（回退），将这一次搜索过程中设置的状态进行清除，从而开始一次新的搜索过程。例如下图示例中，从 f 开始，下一步有 4 种搜索可能，如果先搜索 b，需要将 b 标记为已经使用，防止重复使用。在这一次搜索结束之后，需要将 b 的已经使用状态清除，并搜索 c。

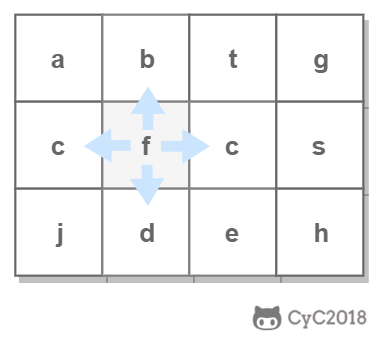
本题的输入是数组而不是矩阵（二维数组），因此需要先将数组转换成矩阵。

public class Solution {
    private final static int[][] next = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};
    private int rows;
    private int cols;

    public boolean hasPath (String val, int rows, int cols, String path) {
        if (rows == 0 || cols == 0) return false;
        this.rows = rows;
        this.cols = cols;
        char[] array = val.toCharArray();
        char[][] matrix = buildMatrix(array);
        char[] pathList = path.toCharArray();
        boolean[][] marked = new boolean[rows][cols];
        for (int i = 0; i < rows; i++)
            for (int j = 0; j < cols; j++)
                if (backtracking(matrix, pathList, marked, 0, i, j))
                    return true;

        return false;
    }

    private boolean backtracking(char[][] matrix, char[] pathList,
                                 boolean[][] marked, int pathLen, int r, int c) {

        if (pathLen == pathList.length) return true;
        if (r < 0 || r >= rows || c < 0 || c >= cols
                || matrix[r][c] != pathList[pathLen] || marked[r][c]) {

            return false;
        }
        marked[r][c] = true;
        for (int[] n : next)
            if (backtracking(matrix, pathList, marked, pathLen + 1, r + n[0], c + n[1]))
                return true;
        marked[r][c] = false;
        return false;
    }

    private char[][] buildMatrix(char[] array) {
        char[][] matrix = new char[rows][cols];
        for (int r = 0, idx = 0; r < rows; r++)
            for (int c = 0; c < cols; c++)
                matrix[r][c] = array[idx++];
        return matrix;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        String val = "ABCESFCSADEE";
        int rows = 3;
        int cols = 4;
        String path = "ABCCED";
        boolean res = solution.hasPath(val, rows, cols, path);
        System.out.println(res);
    }
}